Методи факторного аналізу для оцінки конкурентного середовища фірми

Безліч значень знаходять рішенням характеристичного рівняння - це характеристики варіації, точніше, показники дисперсії кожної головної компоненти. Сумарне значення дорівнює сумі дисперсій елементарних ознак Хj. За умови стандартизації початкових даних, коли рівно числу елементарних ознак m.

Рішення характеристичного рівняння відносно , коли число ознак m достатньо велике і матриця R великої розмірності, викликає труднощі при розрахунку визначника . Вони успішно долаються із застосуванням різноманітних математичних методів матричної алгебри. Найбільш ефективний і легко піддається алгоритмізації серед них метод, що базується на рекуррентных співвідношеннях Фадєєва. Якщо А - деяка симетрична матриця розмірністю m*m, то її визначник знаходиться по сліду матриць, похідних з А формула (2.11):

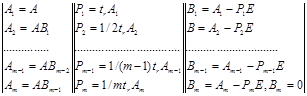(2.11)

На заключному етапі розрахунків Pm і є визначник матриці А (Pm=|A|). Для перевірки обчислень може використовуватися умова: Bm=0.

Після обчислень рекурентних співвідношень записується характеристичний багаточлен:

(2.12)

Значення знаходять після того, як характеристичний багаточлен прирівнюють нулю, одержують характеристичне рівняння і вирішують його щодо характеристичних коренів .- матриця нормованих власних (характеристичних) векторів. Число векторів Vj спочатку рівне m, тобто . Одержують Vj перетворенням ненормованих власних векторів U:

(2.13)

де |Uj| - норма вектора U, тобто:

(2.14)

Необхідність повторного, після отримання матриці R, нормування простору тепер уже узагальнених ознак RF пояснюється механічною появою в ході попередніх розрахунків результатів, що спотворюють нормований простір.

У свою чергу власні вектори Uj знаходять з матричного рівняння:

(2.15)

Реально це означає рішення m систем лінійних рівнянь для кожного при .

В загальному вигляді система рівнянь має формула (2.16):

(2.16)

Приведена вище система об'єднує однорідні лінійні рівняння, і оскільки число її рівнянь дорівнює числу невідомих Umj, має нескінченну безліч рішень. Конкретні значення власних векторів при цьому можна знайти, задаючи довільно принаймні величину однієї компоненти кожного вектора і звичайно, щоб не ускладнювати розрахунків, її прирівнюють одиниці.

Подібні статті по економіці

Аналіз економічного потенціалу підприємства та напрями підвищення ефективності його використання
Проблема підвищення рівня конкурентоспроможності вітчизняного виробництва, наявність конкретних переваг, що виступають гарантом тривалого та ефективного функціонування підприємства в ри ...

Вплив міжнародної торгівлі на розвиток національної економіки
Міжнародна торгівля є формою зв'язку між товаровиробниками різних країн, що виникає на основі міжнародного поділу праці, і виражає їхню взаємну економічну залежність. У літературі часто ...

Адам Сміт як економіст
Прийняти правильне економічне рішення неможливо без глибокого знання економічних законів, що регулюють економічну діяльність, розуміння структури і функцій економічної системи. ...